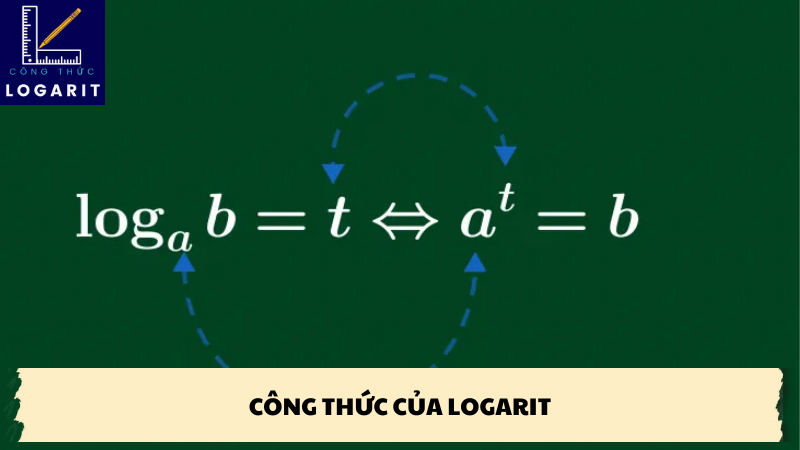Công Thức Của Logarit – 3 Ứng Dụng Thực Tiễn Của Công Thức

Công thức của logarit có những ứng dụng vô cùng thiết thực, ảnh hưởng đến nhiều lĩnh vực khoa học và đời sống ngoài những định nghĩa khô khan .  Bạn sẽ bắt đầu khám phá các bí mật của logarit trong bài viết này, từ các công thức cơ bản nhất đến những ứng dụng thực tế đáng kinh ngạc . 

1. Công thức của logarit cơ bản

Công thức của logarit thông minh nghe có vẻ vật thể , logit thực sự phát hiện từ việc tìm kiếm số mũ, một vấn đề rất cơ bản.  Công thức của logarit được tìm thấy nhiều lần khi biết cơ số và kết quả được phép tăng cường .  Hãy cùng xem xét những “bảng nền tảng ” này . 

Định nghĩa cơ bản về logarit

• Công thức của logarit là phép toán ngược của lũy thừa.  Đặc biệt, trong trường hợp biểu thức a b = c , logarit cơ số a của c sẽlà b.  Nó thường được gọi là log_a(c) = b.  Điều quan trọng là phải là một số dương khác 1, vì mọi lũy thừa của 1 đều bằng 1 , khiến chúng ta không thể phân biệt được các số mũ khác nhau .  Ngoài ra, đối số của logarit, c, phải là một số dương. 
• Việc hiểu rõ định nghĩa này tương tự như việc hiểu chữ cái trước khi đọc một cuốn sách.  Bản chất của logarit không chỉ là những ký hiệu toán học mà còn là một phương pháp mới để giải quyết các vấn đề liên quan đến lũy thừa. 

Cách sử dụng công thức của logarit trong toán học

• Công thức của logarit không liên kết chỉ với các cơ sở toán học được phép ; chúng vẫn là một công cụ hiệu quả để giải quyết các bài toán phức tạp hơn . 
• Công thức của logarit rất quan trọng trong các phương pháp toán và bất kỳ phương trình nào cũng như các bài toán phân tích và đạohàm.

Giải phương trình và bất phương trình logarit

• Chúng tôi thường sử dụng các quy tắc logarit cơ bản trong quá trình giải thích biểu thức, làm cho phương trình trở nên dễ hiểu hơn. Sự thông minh của toán học được thể hiện bằng cách biến một phương trình phức tạp thành một phương trình đơn giản hơn có số ẩn dễ xử lý.
• Tôi phát hiện ra rằng việc giải phương trình và bất phương trình logarit giống với việc giải một trò chơi giải đố. Mỗi bước đi, mỗi thay đổi đều là một quyết định, và chúng ta phải cân nhắc kỹ lưỡng trước khi đưa ra một lời giải đúng đắn. Đôi khi, việc tìm ra lời giải đúng có thể mất thời gian, nhưng cảm giác đạt được lời giải cuối cùng là điều tuyệt vời.

Tính đạo hàm và tích phân của hàm logarit

• Trong quá trình học đạo hàm, việc sử dụng đạo hàm hàm logarit là cần thiết khi chúng ta muốn tìm ra điểm cực trị hoặc tính tốc độ thay đổi của một hàm số phức tạp chứa logarit. Một “bức tranh toàn cảnh” về sự biến thiên của một hàm số được tạo ra sau khi biết đạo hàm của nó.
• Tính đạo hàm và tích phân của hàm logarit không chỉ là việc sử dụng công thức. Đó cũng là một cách để hiểu các mối quan hệ trong toán học. Chúng ta thấy rằng logarit không chỉ là một phép toán trừu tượng mà còn là một phương tiện mạnh mẽ để khám phá những quy luật xã hội và tự nhiên ẩn sâu.

Các bài toán tối ưu hóa sử dụng logarit

• Trong các bài toán tối ưu hóa, trong đó chúng ta cần tìm ra giá trị lớn nhất hoặc nhỏ nhất của một hàm số, công thức của logarit cũng được sử dụng phổ biến. Trong số nhiều loại bài toán tối ưu hóa được sử dụng trong công nghệ và cuộc sống, logarit có thể giúp chúng ta giải quyết chúng một cách dễ dàng.
• Ngoài ra, logarit cũng được sử dụng để tìm giá trị lớn nhất hoặc nhỏ nhất của các biểu thức phức tạp có khó khăn đạo hàm trực tiếp. Chúng ta có thể “biến đổi” bài toán thành một dạng dễ hiểu hơn bằng cách sử dụng các quy tắc logarit.

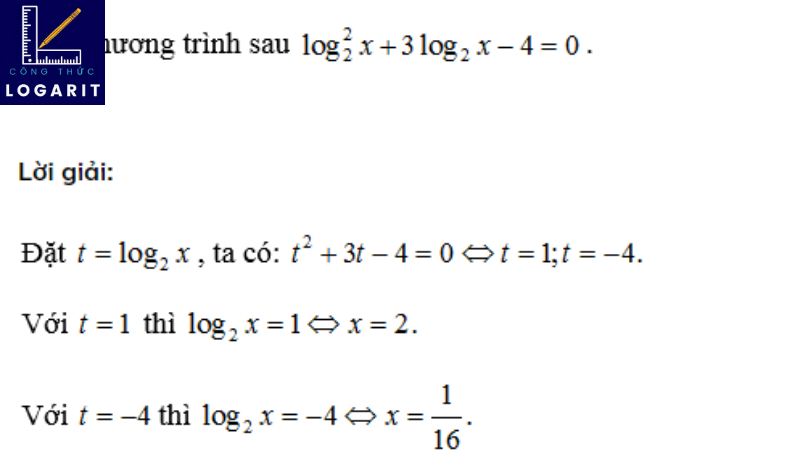
2. Ứng dụng thực tiễn của công thức của logarit

Sau khi nghiên cứu về công thức và ứng dụng của logarit trong toán học, chúng ta sẽ đi sâu vào những ứng dụng thực tế của logarit trong các lĩnh vực khoa học khác nhau. Logaritm không thể thiếu trong mọi lĩnh vực, từ đo độ lớn của động đất và âm thanh đến các bài toán trong tài chính và khoa học máy tính.

Thang đo Logarit trong khoa học tự nhiên

• Tương tự như vậy, độ pH của một dung dịch có thể được tìm thấy bằng cách sử dụng logarit, có dấu âm, của nồng độ ion H+. Điều này giúp chúng ta dễ dàng theo dõi sự khác biệt trong ba giờ giữa các dung dịch mang tính axit. Độ lớn âm thanh cũng được đo bằng decibel (dB), một thang đo logarit được sử dụng để thể hiện sự khác biệt về cường độ âm thanh bằng logarit cơ số 10.
• Tôi phát hiện ra rằng thang đo logarit không chỉ là một phương tiện để đo lường mà còn là một phương tiện giúp chúng ta hiểu rõ hơn về những gì xảy ra trong thế giới tự nhiên. Nó cho phép chúng ta nhận thức được những sự khác biệt tinh tế mà chúng ta có thể không thể nhận thấy nếu chúng ta sử dụng các thang đo thông thường. Thật thú vị khi toán học lại có thể giúp chúng ta có một cách khác để “nhìn” thế giới.

Ứng dụng của logarit trong tài chính và kinh tế

• Công thức của logarit cũng rất quan trọng trong tài chính và kinh tế. Lãi suất kép, ví dụ, tăng trưởng theo cấp số nhân. Chúng ta phải sử dụng công thức logarit để tính toán thời gian cần thiết để một khoản đầu tư tăng lên đến một giá trị cụ thể với lãi suất kép cho trước.
• Tài chính và kinh tế bao gồm logarit, cho thấy toán học không chỉ là một lĩnh vực lý thuyết mà còn là một phương tiện quan trọng để hiểu và giải quyết các vấn đề trong thế giới thực. Điều thú vị là cách các công thức toán học trừu tượng lại có thể trở thành những công cụ mạnh mẽ để giải quyết các vấn đề thực tế có tác động trực tiếp đến cuộc sống của chúng ta.

Logarit trong khoa học máy tính và xử lý dữ liệu

• Công thức của logarit rất quan trọng trong khoa học máy tính, đặc biệt trong việc phân tích độ phức tạp của các thuật toán. Số lượng các phép tính cần thiết để giải một bài toán trong trường hợp tồi tệ nhất tính đến độ phức tạp của thuật toán.
• Logarit cũng được sử dụng trong xử lý tín hiệu và ảnh để tăng cường độ tương phản của ảnh và giải nén dữ liệu. Ứng dụng này minh họa sức mạnh của logarit trong việc thay đổi dữ liệu, làm cho việc xử lý và phân tích dữ liệu trở nên dễ dàng hơn.

3. Các loại công thức của logarit khác nhau

Thế giới Công thức của logarit bao gồm nhiều công thức phức tạp hơn ngoài những công thức cơ bản. Mỗi công thức được sử dụng để giải quyết các bài toán cụ thể. Chúng ta sẽ xem xét một số loại công thức này, từ những loại quen thuộc đến những loại ít được biết đến.

Các công thức logarit nâng cao

• Chúng ta có thể tiếp cận các công thức logarit nâng cao sau khi nắm vững các công thức cơ bản. Một số công thức này rất hữu ích khi giải quyết các bài toán liên quan đến logarit phức tạp, cũng như khi biến đổi biểu thức để dễ dàng giải quyết.
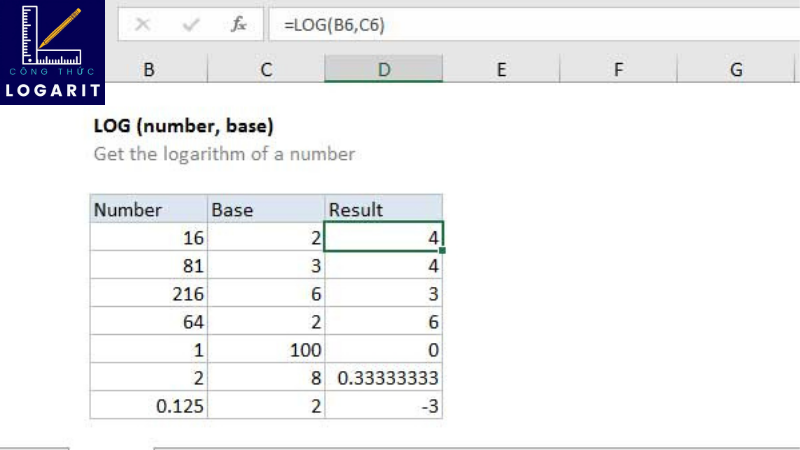
• Công thức đổi cơ số của logarit là một công thức quan trọng. Chúng ta có thể sử dụng công thức này nếu chúng ta có logarit cơ số a của b và chúng ta muốn biến nó thành logarit cơ số c: log_a(b) = log_c(b) / log_c(a). Khi cần tính toán logarit trên các máy tính chỉ có nút logarit cơ số 10 hoặc cơ số e, công thức này rất hữu ích.

Công thức logarit trong giải phương trình vi phân

• Công thức của logarit liên kết giữa một hàm và các đạo hàm của nó được gọi là phương trình vi phân. Khi giải các phương trình vi phân có dạng phân ly biến số, logarit thường xuất hiện. Khi đó, phương trình có thể được đơn giản hóa bằng cách sử dụng logarit cả hai vế hoặc sử dụng hàm số mũ, chẳng hạn như hàm ngược của logarit, để biến nó thành một dạng có thể dễ dàng giải quyết bằng các phương pháp tích phân.
• Khi chúng ta muốn mô tả sự thay đổi của một hệ thống theo thời gian, các phương trình vi phân thường xuất hiện trong nhiều lĩnh vực như vật lý, kỹ thuật và sinh học. Một hàm số để thỏa mãn phương trình vi phân được coi là đã nắm bắt được quy luật của sự thay đổi. Và logarit là một phương tiện quan trọng để làm như vậy.

Mối quan hệ giữa logarit và một số hàm số đặc biệt

• Một số hàm số đặc biệt, chẳng hạn như hàm số mũ, hàm hyperbol và hàm gamma, được liên kết chặt chẽ với logarit.
• Như chúng ta đã biết, hàm ngược của logarit là hàm số mũ. Công thức cho thấy mối quan hệ này: nếu y = e(x), thì x = ln(y). Sự “đối nghịch” này cho thấy hai mặt của một vấn đề cân bằng, cả hai đều quan trọng.
• Các hàm số mũ được sử dụng để định nghĩa các hàm hyperbol. Biểu diễn và nghiên cứu các hàm hyperbol cũng sử dụng logarit. Các hàm hyperbol có nhiều ứng dụng trong các bài toán hình học, vật lý và kỹ thuật. 

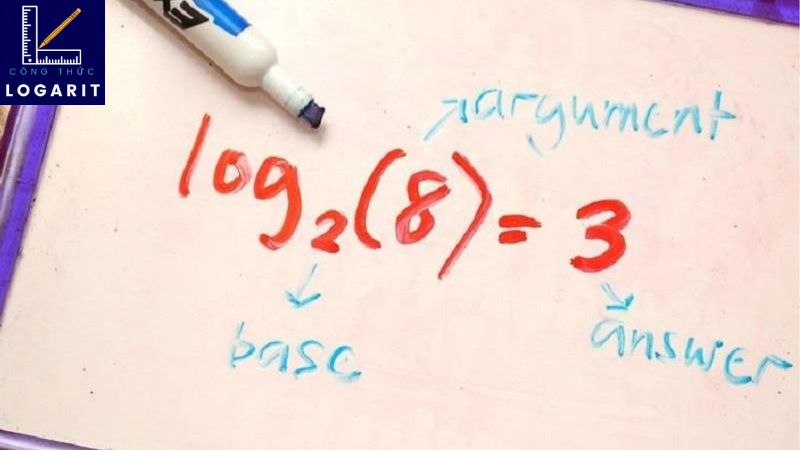
4. Công thức của logarit và sự chuyển đổi giữa các cơ số

Khả năng chuyển đổi giữa các cơ số khác nhau là một đặc điểm quan trọng của logarit. Đặc biệt, khi chúng ta cần so sánh các logarit với các cơ số khác nhau hoặc khi chúng ta cần tính toán logarit bằng các máy tính có giới hạn về cơ số, đây là một công cụ rất hữu ích. Sự linh hoạt của cơ số logarit được thể hiện thông qua việc chuyển đổi.

Công thức chuyển đổi cơ số logarit

• Công thức chuyển đổi cơ số logarit cho phép dễ dàng chuyển đổi từ một cơ số logarit sang một cơ số khác. Công thức này đã được đề cập ở trên, nhưng chúng ta sẽ xem xét cách sử dụng nó và ý nghĩa của nó ở đây. Trong đó, a, b, c là các số dương và a, c khác 1.
• Khi bạn muốn tính logarit cơ số a của b mà máy tính hoặc công cụ tính toán chỉ có chức năng tính logarit cơ số c, bạn có thể tính logarit cơ số c của b và sau đó chia nó cho logarit cơ số c của a theo công thức này. Điều này đặc biệt có lợi khi chúng ta làm việc với những máy tính không có đầy đủ các chức năng tính toán.

Ứng dụng của việc chuyển đổi cơ số trong các bài toán

• Việc chuyển đổi cơ số không chỉ là một hoạt động toán học mà còn là một công cụ tuyệt vời để giải quyết nhiều bài toán phức tạp. Khi chúng ta có một bài toán liên quan đến nhiều logarit với cơ số khác nhau, việc chuyển tất cả chúng về cùng một cơ số sẽ đơn giản hóa và giải quyết bài toán dễ dàng hơn.
• Chúng ta có thể chuyển cả hai logarit về cùng một cơ số và sau đó so sánh chúng trực tiếp khi chúng ta cần so sánh hai logarit có cơ số khác nhau. Ngoài ra, việc chuyển về cùng một cơ số khi giải một phương trình bao gồm nhiều logarit với cơ số khác nhau sẽ giúp chúng ta dễ dàng áp dụng các quy tắc logarit đã học.
• Ngoài ra, khi chúng ta làm việc với các hàm số logarit phức tạp hoặc khi chúng ta muốn biểu diễn một hàm theo một cơ số nhất định để dễ phân tích hơn, việc chuyển đổi cơ số cũng có lợi. Việc chuyển đổi cơ số cho phép chúng ta nhìn thấy các biểu thức logarit linh hoạt và đa dạng hơn.

Sự tương quan giữa các cơ số và ảnh hưởng đến đồ thị hàm logarit

• Giá trị logarit và hình dạng của đồ thị hàm logarit đều bị ảnh hưởng bởi sự thay đổi cơ số logarit. Đồ thị của hàm số logarit có dạng đường cong đi lên dần. Đường cong trở nên “thoải” hơn khi cơ số lớn hơn.
• Các đồ thị của các hàm logarit với các cơ số khác nhau đều đi qua điểm (1,0), vì log(1) = 0. Tuy nhiên, đồ thị sẽ chuyển hướng từ trái sang phải khi cơ số lớn hơn 1, và khi cơ số nằm trong khoảng từ 0 đến 1, nó sẽ chuyển hướng từ trái sang phải.

5. Mối quan hệ giữa công thức của logarit và hàm số mũ

Hàm số mũ và logarit là hai khái niệm thiết yếu, hàm ngược của nhau và không thể thiếu trong các ngành khoa học kỹ thuật. Để hiểu rõ hơn về bản chất của logarit, chúng ta phải tìm hiểu cách chúng liên quan đến hàm số mũ.

Hàm số mũ và định nghĩa ngược của logarit

• Trong đó a là cơ số và x là số mũ, hàm số mũ có dạng y=a+x. Như đã biết, logarit là định nghĩa đảo ngược của hàm số mũ. Chúng ta có thể viết lại y = a^x thành x = log^a(y). Có thể thấy rằng cả hai khái niệm này tương tác với nhau, mang tính chất “thể hiện và giải quyết vấn đề.”
• Llogarit và mũ là các hàm ngược của nhau , nhưng cả hai đều rất quan trọng.  Tùy thuộc vào công cụ toán học , nó cho phép chúng ta hoạt động chuyển từ kết quả sang số mũ hoặc số mũ .​​ Đây là một ví dụ điển hình về sự kết nối chặt chẽ giữa các khái niệm trong toán học.

Tính chất đồ thị và mối liên hệ giữa hai loại hàm

• Mối quan hệ giữa đồ thị logarit và hàm số mũ là đặc biệt. Đồ thị của hai hàm số y = a(x) và y = log(x) trên cùng một hệ trục tọa độ sẽ đối xứng nhau qua đường thẳng y = x.
• Tính chất này là do hai hàm này là hàm ngược của nhau. Nó cho thấy một sự đối xứng hoàn hảo giữa hai đồ thị, chứng minh mối liên hệ chặt chẽ giữa hàm số mũ và logarit. Đồ thị hàm mũ và logarit có thể được coi là biểu tượng của tính chất của hàm.

Ứng dụng liên quan của hàm số mũ và logarit trong thực tế

• Hàm số mũ và logarit có liên quan đến nhiều lĩnh vực khác nhau ngoài toán học. Các mô hình tăng trưởng, chẳng hạn như tăng trưởng dân số, tăng trưởng đầu tư hoặc phân rã phóng xạ, thường sử dụng hàm số mũ. Tuy nhiên, logarit được sử dụng trong các mô hình thang đo và bài toán đo biến thiên lớn.
• Trong các bài toán về lãi suất kép, trong đó chúng ta cần xác định thời gian cần thiết để một số tiền tăng lên một con số nhất định, việc xem xét mối quan hệ giữa hàm số mũ và logarit cũng thường xuyên xảy ra. Chúng ta có thể mô phỏng và giải quyết vấn đề bằng cả hai hàm số này.

6. Kết luận

Với nhiều ứng dụng và công thức đa dạng của mình, Logarit là một công cụ toán học vô cùng quan trọng và mạnh mẽ. Tầm quan trọng của nó đã được chứng minh, từ các công thức cơ bản đến các ứng dụng phức tạp trong toán học, khoa học tự nhiên, tài chính, kinh tế, khoa học máy tính và logarit. Hiểu logarit, cách nó hoạt động và nơi nó được sử dụng , không chỉ giúp họ giải quyết các bài toán mà còn giúp họ hiểu rõ hơn về thế giới bên ngoài .

Việc nắm chắc các quy tắc logarit sẽ hỗ trợ bạn xử lý nhiều bài toán thực tiễn trong khoa học, tài chính và công nghệ. Điều này cũng tương tự như cách mà kiến thức và sự hiểu biết giúp con người tìm ra phương pháp chữa trị và kiểm soát các căn bệnh như bệnh Phong trong lịch sử, chi tiết xin truy cập website congthuclogarit.comcông thức của logarit xin cảm ơn!