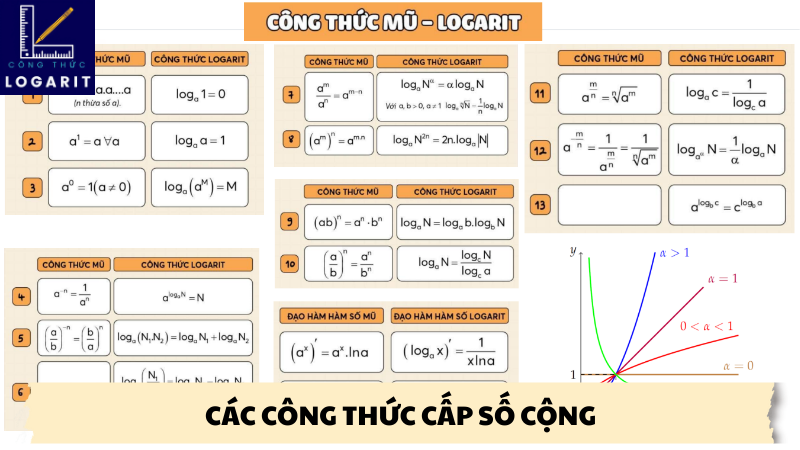
Công thức mũ logarit là một trong những công cụ toán học phổ biến nhất và quan trọng nhất, được sử dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật khác nhau. Nhưng việc áp dụng công thức này không phải lúc nào cũng đơn giản và chính xác. Chúng ta sẽ nói về công thức mũ logarit, cách sử dụng nó, ứng dụng và những sai lầm thường gặp khi sử dụng nó trong bài viết này.
1. Giới thiệu về công thức mũ logarit
Công thức toán học được gọi là “công thức mũ logarit” được sử dụng để tính logarit của một số mũ. Logarit là chỉ số của một mũ mà có thể được nhân để tạo ra một số khác. Chẳng hạn, log_2(8) = 3 vì 2^3 = 8.
Định nghĩa và tính chất của logarit
Logarit là phép toán ngược lại với lũy thừa. Log_a(b) = x khi a^x = b.
Một số đặc điểm cơ bản của logarit là:
- log_a(1) = 0
- log_a(a) = 1
- log_a(ab) = log_a(a) + log_a(b)
- log_a(a^x) = x
2, 10 và e là các cơ sở logarit thường được sử dụng.
Các ứng dụng của công thức mũ logarit
Công thức mũ logarit được sử dụng rộng rãi trong toán học và nhiều lĩnh vực khoa học khác:
- Tính toán giảm giá, tăng trưởng và lãi suất
- Trong phép tính, decibel, âm thanh và điện tử
- trong phân tích thống kê và dữ liệu, chẳng hạn như đo độ entropy
- Lĩnh vực vật lý, hóa học, sinh học và kỹ thuật
- Vì công thức mũ logarit rất quan trọng và được sử dụng rộng rãi, nên việc sử dụng và xử lý các lỗi thường gặp là rất quan trọng.

2. Cách sử dụng công thức mũ logarit trong toán học
Để sử dụng hiệu quả công thức mũ logarit, chúng ta phải hiểu các tính chất cơ bản của logarit và các phép tính liên quan đến nó.
Các phép tính cơ bản với logarit
Một số phép tính cơ bản sử dụng logarit là:
- Giá trị logarit của một số có thể được tính toán như sau: log_a
- Điều chỉnh cơ sở logarit: log_a(b) tương đương với log_c(b) / log_c(a).
- Tích, thương và lũy thừa có thể được tính logarit theo cách sau: Log_a(bc) tương đương với log_a(b) + log_a(c), log_a(b/c) tương đương với log_a(b) – log_a(c), và log_a(b/c) tương đương với c*log_a(b).
- Nắm vững các phép tính này sẽ giúp chúng ta dễ dàng sử dụng công thức mũ logarit trong các bài toán nhất định.
Ví dụ về cách sử dụng công thức mũ logarit
- Ví dụ 1: Giá trị log_2(8). Giải thích: Do 2^3 = 8, log_2(8) = 3.
- Ví dụ 2: Thay đổi log_10(x) thành log_e(x). Giải thích: ln(x) = log_10(x) / log_10(e) = 2.303 *log_10(x).
- Ví dụ 3: Giá trị log_3(81) Giải thích: Do 3^4 = 81, log_3(81) = 4.
- Các ví dụ cho thấy sự cần thiết của việc nắm vững các tính chất và phép tính cơ bản của logarit để có thể sử dụng công thức mũ logarit một cách hiệu quả.
3. Ứng dụng thực tiễn của công thức mũ logarit
Công thức mũ logarit được sử dụng trong nhiều lĩnh vực khoa học và kỹ thuật, bao gồm:
- Trong tính toán lãi suất, tăng trưởng, và giảm giá: Logarit được sử dụng rộng rãi trong các tính toán về lãi suất, giảm giá và tăng trưởng. Chẳng hạn, để tính toán lãi kép, chúng ta có công thức: A = P(1 + r/n)^(nt) trong đó P là số tiền ban đầu, A là số tiền cuối kỳ, r là lãi suất, n là số kỳ tính lãi hàng năm và t là số năm. Để tìm giá trị của t trong trường hợp này, chúng ta có thể sử dụng công thức mũ logarit.
- Trong phân tích decibel, âm thanh, và điện tử: Trong nhiều lĩnh vực, bao gồm điện tử, âm thanh và viễn thông, decibel (dB) là đơn vị đo logarit. Nó được sử dụng rộng rãi trong phân tích decibel, âm thanh và điện tử. Chẳng hạn, để đo cường độ âm thanh, chúng ta sử dụng công thức sau: L = 10log(I/I_0), trong đó I là cường độ âm thanh, và I_0 là cường độ âm thanh thông thường.
- Trong phân tích dữ liệu và thống kê: Logarit cũng được sử dụng trong thống kê và phân tích dữ liệu để xác định các khái niệm như độ đo entropy trong lý thuyết thông tin. Tỷ lệ entropy là H = -Σp_i log(p_i), trong đó p_i là xác suất xảy ra của hiện tượng i. Logarit hỗ trợ định lượng mức độ ngẫu nhiên hay bất định của một biến ngẫu nhiên.
Với những sử dụng quan trọng này, làm quen với công thức mũ logarit là rất quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật.
Các loại công thức mũ logarit phổ biến
Logaritm cơ số 2, logaritm cơ số 10 và logaritm tự nhiên là ba loại công thức mũ logarit phổ biến nhất.
- Logarit cơ số 2 (log_2): Trong lĩnh vực máy tính và khoa học máy tính, logarit cơ số 2 thường được sử dụng vì nó liên quan trực tiếp đến bit, đơn vị cơ bản của thông tin số. Chẳng hạn, log_2(8) = 3 vì 2^3 = 8.
- Logarit cơ số 10 (log_10): Loại logarit phổ biến nhất là logarit cơ số 10, thường được sử dụng trong các lĩnh vực khoa học và kỹ thuật. Hệ thập phân liên quan trực tiếp đến nó. Để minh họa, log_10(1000) = 3, vì 10×3 = 1000.
- Logarit tự nhiên (ln hoặc log_e): Logarit tự nhiên, còn được gọi là logarit neperien, là một hằng số toán học quan trọng có giá trị khoảng 2.718. Lý thuyết xác suất và các mô hình toán học thường sử dụng logarit tự nhiên. Vì e^1 = e, nên ln(e) = 1.
Vì mỗi loại logarit có mục đích riêng, nên việc hiểu các loại logarit phổ biến sẽ giúp chúng ta lựa chọn và sử dụng công thức mũ logarit một cách hiệu quả.
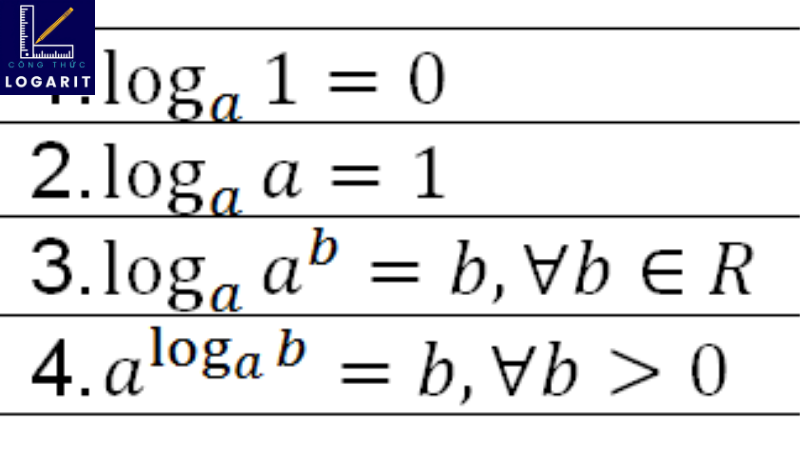
4. Ví dụ minh họa công thức mũ logarit
Chúng ta sẽ xem xét một số ví dụ cụ thể để hiểu rõ hơn về cách sử dụng công thức mũ logarit.
Tính toán lãi suất sử dụng công thức mũ logarit
Giả sử bạn gửi một nghìn đồng với lãi suất 5% hàng năm. Số tiền sẽ tăng gấp đôi sau bao nhiêu năm?
Chúng ta tính toán bằng công thức sau: A = P(1 + r/n)^(nt), trong đó:
- A là số tiền cuối kỳ
- P là số tiền gửi ban đầu
- r là lãi suất (5% = 0.05)
- n là số lần tính lãi trong một năm (ở đây là 1)
- t là số năm
Tìm t sao cho A = 2P. Thay vì sử dụng công thức, chúng ta có 2P = P(1 + 0.05/1).1t/2 = (1.05)^Tính toán t log_10(2) = t*log_10(1,05) t = log_10(2) / log_10(1.05) tương đương với 13.98 năm. Sau 14 năm, số tiền sẽ tăng gấp đôi.
Tính toán cường độ âm thanh bằng decibel
Đơn vị decibel (dB) thường được sử dụng để đo cường độ âm thanh. Điều này có thể được tìm thấy bằng cách sử dụng công thức sau: L = 10log(I/I_0), trong đó:
- L là mức độ âm thanh tính bằng decibel.
- I là cường độ âm thanh,
- I_0 là cường độ âm thanh chuẩn.
- Ví dụ, nếu I = 1 W/m^2 và I_0 = 10^-12 W/m^2, thì mức cường độ âm thanh sẽ là L = 10log(1/10^-12) = 10log(10^-12) = 120 dB.
- Do đó, công thức mũ logarit là một phương pháp quan trọng để tính toán và đo cường độ âm thanh.
- Chúng ta có thể thấy từ các ví dụ rằng công thức mũ logarit có thể được sử dụng một cách linh hoạt trong nhiều ứng dụng thực tiễn khác nhau.

5. Những sai lầm thường gặp khi áp dụng công thức mũ logarit
Mặc dù công thức mũ logarit là một công cụ toán học mạnh mẽ, nhưng đôi khi có những sai lầm thường gặp khi sử dụng nó. Đây là một số sai lầm phổ biến nhất:
- Nhầm lẫn giữa logarit cơ số khác nhau: Nhầm lẫn giữa các cơ sở logarit là một lỗi phổ biến. Ví dụ: sử dụng log_10 thay vì log_2 hoặc log_e. Điều này có thể có kết quả hoàn toàn khác.
- Sử dụng sai công thức mũ logarit: Có khả năng một cá nhân sử dụng sai công thức mũ logarit, ví dụ: log_a(b^c) = b*log_a(c) thay vì log_a(b^c) = c.:*log_a(b)
- Nhầm lẫn giữa logarit và lũy thừa: Một lỗi khác là nhầm lẫn giữa logarit và lũy thừa. Ví dụ, có khả năng log_2(8) = 2 không phải là 3.
Việc hiểu rõ các tính chất và cách sử dụng chính xác công thức mũ logarit là rất quan trọng vì những sai lầm này có thể dẫn đến kết quả sai lệch đáng kể.
6. Kết luận
Chúng tôi đã tìm hiểu về công thức mũ logarit, một công cụ toán học quan trọng và phổ biến có nhiều ứng dụng thực tiễn trong các lĩnh vực khoa học và kỹ thuật khác nhau, trong bài viết này. Chúng tôi đã nghiên cứu các khái niệm cơ bản về logarit, bao gồm cách sử dụng công thức mũ logarit và các loại logarit.
Tuy nhiên, dù là toán học hay trong cuộc sống, chúng ta cũng không nên bỏ qua các vấn đề sức khỏe quan trọng như bệnh sán chó – một bệnh lý cần được quan tâm và phòng ngừa kịp thời, chi tiết xin truy cập website congthuclogarit.com xin cảm ơn!