Một trong những kiến thức cơ bản và cần thiết trong chương trình toán học lớp 6 là lũy thừa. Việc nắm vững các công thức lũy thừa không chỉ giúp học sinh giải quyết bài toán nhanh chóng mà còn tạo nền tảng vững chắc cho những kiến thức nâng cao sau này khi giáo dục phát triển và yêu cầu học tập ngày càng khắt khe. Chúng tôi sẽ nói về 5 công thức lũy thừa lớp 6 trong bài viết này. Chúng tôi sẽ giúp các bạn học sinh có thêm tài liệu tham khảo và áp dụng chúng vào thực tiễn học tập.
1. Giới thiệu về 5 công thức lũy thừa lớp 6
Ý tưởng về lũy thừa bao gồm số lần nhân của một số với chính nó. Trong toán học, lũy thừa được mô tả bằng dạng “a^n”, trong đó “a” là một cơ số (còn được gọi là “số bị lũy thừa”) và “n” là một số mũ, được sử dụng để hiển thị số lần nhân. Học lũy thừa sẽ giúp học sinh hiểu được các phép toán phức tạp hơn như căn bậc hai và các biểu thức đại số.
5 công thức lũy thừa lóp 6 mà chúng ta sẽ xem xét bao gồm các quy tắc cơ bản giúp tính toán và giải quyết các bài toán liên quan đến lũy thừa trở nên dễ dàng hơn. Những công thức này không chỉ được sử dụng trong lý thuyết mà còn có thể được áp dụng trong nhiều bài toán thực tế.
Khám phá chi tiết từng công thức và cách áp dụng chúng trong quá trình học tập cùng nhau nhé!
2. Khái niệm lũy thừa trong toán học
Nhiều lĩnh vực khác, chẳng hạn như đại số, hình học và phân tích, dựa trên lũy thừa trong toán học. Biểu diễn các số lớn hoặc phép toán phức tạp được đơn giản hóa nhờ khái niệm này.
Định nghĩa của “lũy thừa”
- Một phép nhân lặp lại được gọi là lũy thừa. Cụ thể, trong trường hợp một số nguyên dương (n) và một số số (a), lũy thừa của số số (a) theo số nguyên dương (n) được viết là a^n và có thể được hiểu là số số (a) được nhân với chính nó (n). Chẳng hạn, (2×3 = 2×2 = 8).
- Cũng có thể sử dụng lũy thừa cho các số âm và số 0. Lũy thừa được tính là (frac{1}{a^{-n}} khi n = 0 và a = 1 với mọi số a khác 0.
Cấu trúc của phép lũy thừa
- Cơ số và số mũ là hai thành phần chính của một phép lũy thừa. Cơ số là số bạn muốn nhân, và số mũ là số lần. Điều này có nghĩa là bạn phải hiểu cả hai yếu tố để hiểu rõ về lũy thừa.
- Ví dụ, trong phép lũy thừa (3×4), số 3 là một cơ số và 4 là một số mũ, vì vậy bạn sẽ nhân số 3 với chính nó bốn lần: ( 3 x 3 x 3 x 3 = 81 ).
Ý nghĩa của việc có lũy thừa trong cuộc sống
- Lũy thừa không chỉ được tìm thấy trong sách giáo khoa mà còn có lợi trong cuộc sống hàng ngày. Chẳng hạn, bạn thường phải sử dụng các phép lũy thừa khi cần tính diện tích hoặc thể tích của một hình khối. Tính toán trở nên nhanh chóng và dễ dàng hơn nhờ lũy thừa.
- Ngoài ra, lũy thừa là một khái niệm phổ biến trong lập trình và công nghệ thông tin. Các thuật toán thường xuyên sử dụng lũy thừa để xử lý dữ liệu, chẳng hạn như mã hóa, bảo mật dữ liệu hoặc lưu trữ dữ liệu.
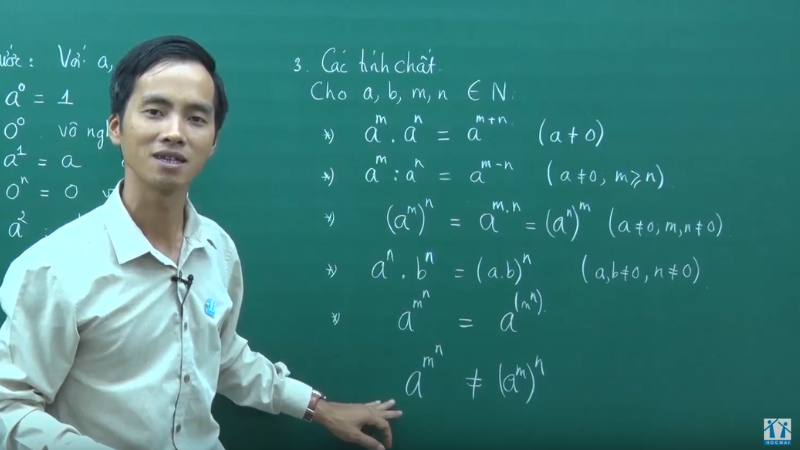
3. Công thức lũy thừa của một số tự nhiên
Học sinh toán lớp sáu sẽ làm quen với một số công thức lũy thừa cơ bản. Học sinh không chỉ có thể hoàn thành bài tập nhanh hơn mà còn có thể hiểu rõ hơn về các mối quan hệ giữa các số trong tự nhiên.
Công thức lũy thừa của các số có nguồn gốc tự nhiên
- Học sinh phải ghi nhớ một số công thức lũy thừa cơ bản. Một trong số đó bao gồm:
- Mỗi số lũy thừa có số mũ bằng 1 đều bằng chính nó.
- Mọi số lũy thừa có số mũ bằng 0 đều bằng 1, ngoại trừ 0.
- Định nghĩa cơ bản của bình phương của một số là (a^2 = a x a).
- Những công thức này đơn giản nhưng rất quan trọng vì chúng cung cấp nền tảng cho việc hiểu rõ hơn về các phép toán phức tạp hơn và lũy thừa.
Các đặc điểm của lũy thừa
- Ngoài các công thức cơ bản, học sinh nên nắm rõ một số đặc điểm quan trọng của lũy thừa:
- Đặc điểm của phép nhân: (a^{m+n} = a^m x a^n)
- Phép chia có tính chất là ( \frac{a^m}{a^n} = a^{m-n} ).
- Tính chất của lũy thừa là ((a^m)n = a{m x n}.
- Các tính năng này không chỉ giúp học sinh giảm bớt công việc tính toán mà còn giúp họ hiểu phép lũy thừa từ nhiều quan điểm.
Một ví dụ cho thấy
- Chúng ta có thể xem xét một số ví dụ cụ thể để làm rõ hơn về các công thức và tính chất lũy thừa. Học sinh có thể thấy từ các ví dụ này rằng lũy thừa có thể được sử dụng rất tốt trong toán học. Ví dụ, nếu (a = 2) và (m = 3), hãy tính (a^m): (a^m = 2^3 = 2 times 2 times 2 = 8) và nếu (m = 3) và (n = 2), hãy tính
4. Áp dụng 5 công thức lũy thừa lớp 6 trong bài toán
Một kỹ năng rất quan trọng để giải quyết bài toán thực tế là sử dụng 5 công thức lũy thừa lớp 6. Nó không chỉ cải thiện khả năng tư duy của học sinh mà còn khơi dậy niềm đam mê toán học của họ.
Biểu thức thay đổi
- Biến đổi biểu thức đại số là một trong những ứng dụng chính của lũy thừa. Học sinh có thể sử dụng công thức lũy thừa để đơn giản hóa trước khi tính toán khi biểu thức trở nên phức tạp.
- Học sinh có thể đơn giản hóa biểu thức ( 3^2 x 3^3) bằng cách sử dụng tính chất của phép nhân: [ 3^2 x 3^3 = 3^{2+3} = 3^5 = 243 ].
Giải quyết bài toán dựa trên hình học
- Khi giải các bài toán hình học, lũy thừa rất quan trọng, đặc biệt là các bài toán liên quan đến diện tích và thể tích. Học sinh sẽ sử dụng công thức [S = a^2] để tính diện tích của một hình vuông. ] Trong đó diện tích (S) và chiều dài cạnh của hình vuông (a).
- Tương tự như vậy, khi tính thể tích của một hình lập phương được tìm thấy, công thức sẽ là: [V = a^3 ] Nơi thể tích (V) và chiều dài cạnh (a).
Giải quyết bài toán ứng dụng trong thế giới thực
- Lũy thừa có thể được sử dụng trong các bài toán thực tế và trong lý thuyết. Ví dụ, học sinh có thể thực hiện một bài toán liên quan đến tốc độ phát triển của một cây cối và tìm thấy các công thức lũy thừa để dự đoán thời gian cần thiết để cây đạt được chiều cao nhất định.
- Điều này cho thấy rằng việc sử dụng lũy thừa trong các bài toán đời sống thúc đẩy sự sáng tạo và tư duy phản biện của học sinh.

5. Làm quen với 5 công thức lũy thừa lớp 6 cơ bản
Học sinh cần làm quen và tập luyện kỹ lưỡng để có thể làm chủ 5 công thức lũy thừa lớp 6. Họ không chỉ giải quyết bài tập tốt hơn mà còn có sự tự tin hơn khi đối mặt với các câu hỏi khó.
Công thức lũy thừa tổng thể
- Như đã nói, học sinh cần ghi nhớ một số công thức lũy thừa cơ bản. Họ sẽ giải quyết bài tập một cách nhanh chóng và chính xác hơn nếu họ nắm vững những công thức này.
- Lũy thừa tích: [(ab)^n = a^n x b^n]
- Lũy thừa của vết thương: [ frac{a}{b} ][^n = \frac{a^n}{b^n}]
- Học sinh có thể hiểu rõ hơn về cách xử lý các phép toán lũy thừa phức tạp với những công thức này.
Trải nghiệm với các bài toán đơn giản
- Học sinh nên bắt đầu với các bài toán đơn giản liên quan đến công thức lũy thừa trước khi tiến hành các bài toán phức tạp hơn. Họ phát triển tư duy logic và xây dựng nền tảng vững chắc nhờ cách làm này.
- Ví dụ: Tính ((2 x 3)^2)
- Giải bài toán: Tìm giá trị (x) nếu (2x = 16).
Hình thành thói quen ôn tập
- Học sinh phải có thói quen ôn tập thường xuyên để tránh quên những gì họ đã học. Ôn tập không chỉ nâng cao kiến thức của họ mà còn khiến họ cảm thấy tự tin hơn khi tham gia các kỳ thi hoặc kiểm tra.
- Học sinh thậm chí có thể tìm kiếm các ứng dụng hoặc trang web hỗ trợ luyện tập lũy thừa trực tuyến hàng ngày để tăng cường khả năng học tập.
6. Phương pháp giải toán với 5 công thức lũy thừa lớp 6
Giải toán lũy thừa là một kỹ năng cần học. Để giải quyết các bài toán lũy thừa một cách hiệu quả, học sinh cần nắm vững một số kỹ thuật sau đây.
Đánh giá bài toán
- Phân tích bài toán rất quan trọng trước khi bắt tay vào giải. Học sinh phải tìm hiểu các yêu cầu và công thức cần thiết cho bài toán.
- Đôi khi, việc phân chia bài toán thành các phần nhỏ hơn có thể giúp giải quyết nó dễ dàng hơn. Hãy hỏi: “Cần tìm cái gì?”và “Thông tin đã được đưa ra là gì?”
Sử dụng bảng biểu hoặc sơ đồ
- Đôi khi, học sinh có thể dễ dàng hình dung được vấn đề mà bài toán đặt ra bằng cách sử dụng sơ đồ hoặc bảng biểu. Điều này không chỉ giúp tổ chức thông tin chính xác mà còn giúp xác định các mối quan hệ giữa các thành phần của bài toán.
- Học sinh có thể lập bảng để so sánh các chiều dài và diện tích tương ứng khi tính diện tích hình chữ nhật. Điều này giúp học sinh dễ dàng tìm ra mối quan hệ và tính toán kết quả.
Xem lại kết quả.
- Sau khi hoàn tất bài toán, hãy kiểm tra lại kết quả. Học sinh nên kiểm tra kết quả với các giá trị họ đã biết hoặc sử dụng các phương pháp khác để đảm bảo rằng kết quả là chính xác.
- Nếu bạn có thời gian, hãy thử giải bài toán bằng một phương pháp khác để xem liệu bạn có đạt được cùng một kết quả hay không. Bạn không chỉ tự tin hơn mà còn hiểu rõ hơn về vấn đề.

7. Kết quả:
Chương trình toán lớp sáu phải bao gồm lũy thừa. Nắm vững 5 công thức lũy thừa lớp 6 sẽ giúp học sinh giải nhanh các bài toán khó và tạo nền tảng vững chắc cho những kiến thức nâng cao hơn trong tương lai. Có lẽ qua bài viết này, bạn đã có cái nhìn rộng hơn về lũy thừa, từ khái niệm đến các ứng dụng thực tế. Bạn sẽ thấy mình tiến bộ hơn trong toán nếu bạn dành thời gian luyện tập và ôn tập. Nếu nhà bạn có trẻ con thì hãy tìm hiểu về bệnh tay chân miệng để phòng chống cho trẻ.
Trên đây là bài viết về 5 công thức luỹ thừa lớp 6, chi tiết xin truy cập vào website: congthuclogarit.com xin cảm ơn.
